单调栈

发表于 | 分类于 |

单调栈

定义

单调栈就是满足单调性的栈结构。

性质

  • 单调栈里的元素具有单调性；
  • 每个元素在入栈前，将栈顶破坏栈单调性的元素都出栈；
  • 使用单调栈可以找到入栈时元素向左遍历到的第一个比他小（大）的元素；出栈时元素向右遍历第一个比他小（大）的元素。（做题大多依靠这条性质）

例题

739 每日温度

题目描述

请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

原题链接

解释

这道题思路比较明显，找每一个数右边第一个比他大的数。所以可以使用单调栈实现。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[] dailyTemperatures(int[] T) {
        Deque<Integer> I=new ArrayDeque<>();
        int[] result=new int[T.length];
        if (T.length==0){
            return result;
        }
        I.addLast(0);
        for (int i=1;i<T.length;i++){
            int tempT=T[i];
            while (!I.isEmpty() && T[I.getLast()]<tempT){
                int pI=I.removeLast();
                result[pI]=i-pI;
            }
            I.addLast(i);
        }
        if (!I.isEmpty()){
            for (int i:I
                 ) {
                result[i]=0;
            }
        }
        return result;
    }
}

84 柱状图中最大的矩形

题目描述

给定n个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。求在该柱状图中，能够勾勒出来的矩形的最大面积。  

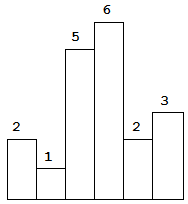LearningGp 以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

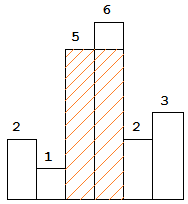overwrote existing file 图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10个单位。 原题链接

解释

每个能勾勒出的矩形其实可以理解成为其中最短的一个柱体向左右拓展。所以暴力枚举方法为:

  • 枚举某一柱子
  • 向左右拓展直到遇到高度小于其的柱子停止
  • 计算面积

但是我们可以发现这边其实要找的就是某一柱子的左边以及右边第一个比它矮的柱子，这个需求非常符合单调栈的第三条性质。所以这题可以使用单调栈来优化解决。将每个柱体依次入栈，若当前的柱体高度大于等于栈顶柱体的高度，就直接将当前柱体入栈，否则当前栈顶的柱体就找到了右边的第一个小于自身的柱体（右边界），而对栈中柱体来说，栈中的下一个柱体就是其左边第一个小于自身的柱体（左边界）那么就可以将栈顶柱体出栈并计算面积。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);
        
        Stack<Integer> stack = new Stack<Integer>();
        for (int i = 0; i < n; ++i) {
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                right[stack.peek()] = i;
                stack.pop();
            }
            left[i] = (stack.isEmpty() ? -1 : stack.peek());
            stack.push(i);
        }
        
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

42 接雨水

题目描述

给定n个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。  

LearningGp 示例: 输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6 原题链接

解释

这题依旧可以看出是寻找边界的题目。栈顶元素是左边界，当前柱体是右边界，当前高度是两者高度中的较小者减去计算过的高度。详解来自Sweetiee

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        int res = 0;
        // 遍历每个柱子
        for (int i = 1; i < height.length - 1; i++) {
            int leftMax = 0, rightMax = 0;
            // 计算当前柱子左侧的柱子中的最大高度
            for (int j = 0; j <= i; j++) {
                leftMax = Math.max(leftMax, height[j]);
            }
            // 计算当前柱子右侧的柱子中的最大高度
            for (int j = i; j < height.length; j++) {
                rightMax = Math.max(rightMax, height[j]);
            }
            // 结果中累加当前柱子顶部可以储水的高度，
            // 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
            res += Math.min(leftMax, rightMax) - height[i];
        }
        return res;
    }
}

关于Deque

在这篇文章给出的代码中有些使用了Deque代替stack，或是对Deque进行一次封装代替stack。原先的stack不符合OOP设计原则。虽然stack仍未被弃用，且在算法题中影响不大，但是确实Deque作为双端队列更加方便，但如果出于封装性的考虑，可以对Deque再做一次封装，限制非栈操作。详细解释