并查集

发表于 | 分类于 |

概念

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作：

  • 查找（Find）：确定某个元素处于哪个子集；
  • 合并（Union）：将两个子集合并成一个集合。

结构

在理解上并查集是一个森林，但是在实际实现上位了方便将其简化成数组。

理解上的结构

结构

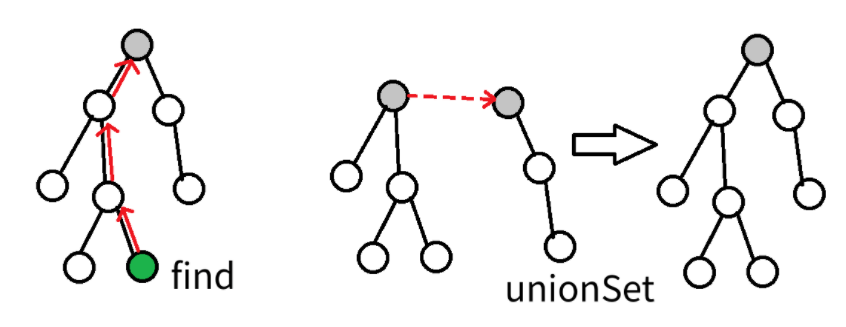
每棵树代表一个子集，根节点用来标记这个子集

操作

  • find：递归查找父节点，最终得到标记子集的根节点（祖先）
  • union：将两棵树合并（不必在意细节，因为实现时使用数组）

实际的实现

结构

我们使用一个parent数组来存储对应索引的父亲的索引

1
2
3
4
//初始化代码,一开始每个节点一个子集，自己的父亲为自己
for (int i = 0; i < n; i++) {
	this.parent[i] = i;
}

操作

  • find操作，递归查找父节点，最终得到标记子集的根节点（祖先）
1
2
3
4
5
6
7
8
9
public int find(int x) {
  // 寻找x的祖先
  if (parent[x] == x) { // 如果x是祖先则返回
    return x;
	}
  else {
    return find(parent[x]); // 如果不是则x的爸爸问x的爷爷
	}  
}
  • union操作，合并子集
1
2
3
4
//使两个集合拥有相同的祖先
public void union(int x,int y){
	parent[find(x)]=find(y);
}

优化

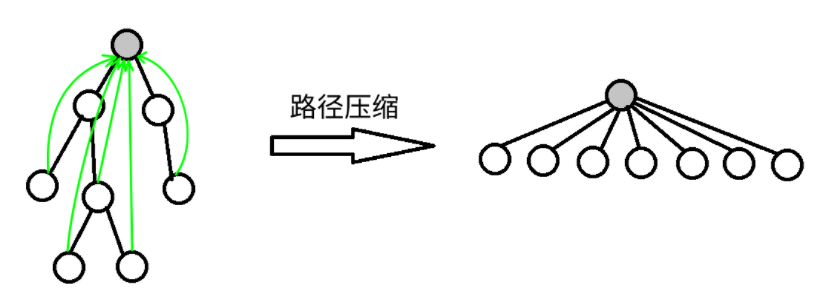
路径压缩

概念

把每个节点都直接连接到根上 ，这就是路径压缩（把递归查找祖先的路径压缩）

实现

1
2
3
4
5
6
public int find(int x) {
	if (x != parent[x]) {
		parent[x] = find(parent[x]); //把寻找祖先路上经过的节点都压缩
	}
	return parent[x];
}

启发式合并（按秩合并）

概念

简单来说在合并时将深度（或者节点个数）较小的合并子集到较大的子集中去

需要一个rank数组来粗略的记录深度（主要是为了方便，没必要精确记录深度）

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//初始化rank数组
for (int i = 0; i < n; i++) {
	this.rank[i] = 1;
}

public void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX == rootY) {
        return;
    }

    if (rank[rootX] == rank[rootY]) {
        parent[rootX] = rootY;
        // 此时以 rootY 为根结点的树的高度仅加了 1
        rank[rootY]++;
    } else if (rank[rootX] < rank[rootY]) {
        parent[rootX] = rootY;
        // 此时以 rootY 为根结点的树的高度不变
    } else {
        // 同理，此时以 rootX 为根结点的树的高度不变
        parent[rootY] = rootX;
    }
}

总体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
private class UnionFind {

    private int[] parent;
    /**
     * 以 i 为根结点的子树的高度（引入了路径压缩以后该定义并不准确）
     */
    private int[] rank;

    public UnionFind(int n) {
        this.parent = new int[n];
        this.rank = new int[n];
        for (int i = 0; i < n; i++) {
            this.parent[i] = i;
            this.rank[i] = 1;
        }
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX == rootY) {
            return;
        }

        if (rank[rootX] == rank[rootY]) {
            parent[rootX] = rootY;
            // 此时以 rootY 为根结点的树的高度仅加了 1
            rank[rootY]++;
        } else if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
            // 此时以 rootY 为根结点的树的高度不变
        } else {
            // 同理，此时以 rootX 为根结点的树的高度不变
            parent[rootY] = rootX;
        }
    }

    public int find(int x) {
        if (x != parent[x]) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
}

复杂度

oi-wiki-并查集

References

oi-wiki-并查集
leetcode-1202题解